ПРОБЛЕМЫ ИНТЕГРАЛЬНЫХ ОЦЕНОК ТЕХНИЧЕСКИХ СИСТЕМ
В.Е.Минакер, М.В.Быховский
Метод обобщенных или интегральных оценок объектов, характеризуемых качественно неоднородными параметрами, широко используется во многих областях, в частности, при исследовании ситуаций (наименее разработанной в классической ТРИЗ области). В ТРИЗ он используется, например, для определения показателя идеальности ТС. Анализируются особенности метода, пренебрежение которыми приводит к наиболее распространенным ошибкам. Показывается, что результаты его применения часто оказываются недостаточно точными.
Идеальность, техническая система (ТС), функция, свойство, параметр, интегральная оценка.
Главным мотивом деятельности Г.С. Альтшуллера при создании ТРИЗ было желание создать методы решения проблем в техносфере, которые резко снизили бы количество и цену ошибок. Он полагал, что добиться этого позволит замена случайного перебора вариантов алгоритмическим методом решения изобретательских задач. [1] К сожалению, после создания классической ТРИЗ к концу 80-х годов прошлого века проблема ошибок не стала менее острой. Здесь следует отметить, что реальная инновационная деятельность не сводится только к решению изобретательских задач. Кроме того, при их решении далеко не всегда используется случайный перебор вариантов, поэтому он является не единственной причиной ошибок. Значительная их часть совершается до и после решения задач, а именно при исследовании ситуаций. [2] Эта область в классической ТРИЗ почти не разработана. Одной из важных проблем при анализе ситуаций является оценка ТС и определение лучшей из них. Эту процедуру приходится выполнять, например, при определении ТС, подлежащей совершенствованию, направлений этого совершенствования, а также перспективности инновационных решений.
С необходимостью оценки объектов, характеризуемых неоднородными параметрами, каждый человек сталкивается достаточно часто. Например, приобретая даже самые простые товары, необходимо оценивать и сравнивать большое количество неоднородных параметров (вес, размер, цвет, механические свойства и т.д.). Чаще всего такую оценку человек делает интуитивно и при этом нередко грубо ошибается. Для уменьшения ошибок при исследовании ситуаций разработаны методы экспертных оценок. [3] Сравнивать несколько ТС, основываясь только на качественных оценках, часто бывает трудно. Поэтому для упрощения сравнения ТС используются количественные оценки. При этом каждой качественной оценке присваивают определенный балл. После этого ТС могут сравниваться по численным оценкам параметров. Если ТС характеризуется большим числом параметров, достаточно часто используются обобщенные (интегральные) оценки. Они применяются в распространенных методах анализа ситуаций, например, в функционально-стоимостном анализе, бенчмаркинге, методе структурирования функций качества, а также при определении качества пищевых продуктов. [4-8]. Как правило, в качестве интегральной оценки принимается арифметическая сумма оценок частных параметров: ![]()
где
П? - интегральная оценка объекта,
Пi - оценка i-го параметра.
Одной из проблем интегральных оценок является необходимость учесть неодинаковую важность частных параметров. Как правило, эту проблему решают введением коэффициентов весомости параметров. Каждому параметру методом экспертных оценок присваивается весовой коэффициент, отражающий его важность в конкретной ситуации. Тогда формула (1) для расчета интегральной оценки принимает вид: ![]()
где ki - весовой коэффициент i-го параметра.
В некоторых случаях применяется умножение оценок частных параметров, в частности оно использовалось Г.С. Альтшуллером [9]: ![]()
Очевидно, что при сравнении нескольких ТС с расчетом интегральных оценок по формуле (3) коэффициенты весомости можно не вводить, что, на первый взгляд, указывает на преимущество этого метода вычисления.
Во многих случаях для интегральной оценки используют отношение суммы оценок частных параметров, например, к затратам, выраженным в денежных или других единицах, а также обратные им величины. Известным примером удельной интегральной оценки является показатель цена/качество, на который эксперты советуют ориентироваться покупателям. Примером удельной интегральной оценки в ТРИЗ является показатель идеальности ТС [10]: 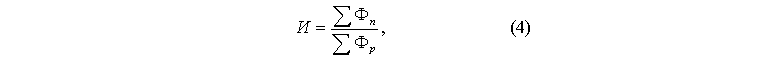
где
И - показатель идеальности ТС,
Фn - сумма выполняемых ТС полезных функций,
Фр - сумма факторов расплаты.
Помимо арифметического суммирования или умножения оценок частных параметров ТС могут применяться другие способы вычисления обобщенных оценок, например, суммирование квадратов оценок частных параметров: ![]()
Следует отметить, что при сравнении нескольких ТС, интегральные оценки которых расчитываются различными способами, ранжирование может давать неодинаковые результаты. Например, при сравнении ТС1 и ТС2 оценки параметров меняются от 1 до 5, а оценки коэффициентов весомости от 1 до 3. Баллы подобраны так, чтобы интегральные оценки, рассчитанные по формуле (2), совпадали. Результаты расчета интегральных оценок сведены в таблицу 1. 
Как видно из результатов, представленных в таблице 1, при использовании формулы (2) у TC1 и TC2 ранг одинаковый (20 = 20). А при использовании формул (3) и (5) ранг у TC1, соответственно, меньше (75 < 200) и больше (11,49 > 10,1) чем у TC2. В связи с этим возникает вопрос о том, какое ранжирование является правильным. До тех пор, пока выбор формулы для расчета интегральной оценки не будет иметь строго теоретического обоснования, этот вопрос останется открытым.
Поскольку метод интегральных оценок широко применяется, в том числе в инновационной деятельности, обсудим наиболее простые положения, вытекающие из теории измерений, пренебрежение которыми приводит к наиболее распространенным ошибкам.
Как известно, любые измерения производятся не абсолютно точно. При оценке экспертами качественных характеристик существует четыре вида погрешностей. Два из них связаны с применяемыми шкалами, а еще два - это случайные и систематические погрешности экспертов.
Первый вид погрешностей вносится инструментом измерения, т.е. балловыми шкалами оценок [3, 11-12]. При экспертной оценке частных параметров и коэффициентов весомости используются шкалы как с целыми, так и с дробными числами. Шкалы, представляющие собой упорядоченную совокупность чисел и качественных характеристик оцениваемых объектов, служат для перевода качественных характеристик в количественные. Численным баллам соответствуют качественные уровни, которые описываются словесно. Чаще всего шкалы начинаются с первого уровня, которому соответствует максимально низкая оценка свойства, но иногда встречаются шкалы, начинающиеся с нулевого уровня, которому соответствует отсутствие свойства. [3-5] Примеры соответствия баллов и качественных уровней приведены в таблице 2. 
Качественные и соответственно количественные оценки параметров, как и их важность, подвержены изменениям. Эти изменения наиболее очевидно зависят от ситуаций использования оцениваемых ТС. При постепенном изменении ситуации, например экономической, оценка "хорошо" постепенно может меняться к оценке "удовлетворительно" или оценке "отлично".
При назначении качественных и количественных оценок эксперт подобно измерительному прибору "измеряет" частный параметр ТС. При этом он пользуется "шкалой", имеющей "цену деления", соответствующую разнице между соседними баллами, которая определяются чувствительностью эксперта. Он округляет промежуточные оценки до значений, соответствующих "делениям" на "шкале", как и при использовании измерительного прибора.
Это в определенной степени относится и к коэффициентам весомости, учитывающим важность параметров. Как и при оценке параметров, при оценке их важности можно говорить об измерении коэффициентов весомости параметров и шкалах для такого измерения. Разница между оценкой параметров и оценкой коэффициентов их важности, в частности, состоит в том, что оценки параметров во многих случаях можно прямо или косвенно соотнести с объективными свойствами, а оценки важности являются сугубо субъективными. Наряду с субъективными предпочтениями на оценку важности параметра, в первую очередь, влияют ситуации использования ТС. Например, важность параметров, характеризующих красоту и удобство одежды в случае ее использования на официальном мероприятии и в сложном путешествии, будет неодинаковой. Здесь, как и в случае самих параметров, можно различать "истинное" значение коэффициента весомости параметра и значение, округленное до уровня на шкале.
Известно несколько способов округления истинных значений при измерении. Наиболее часто применяется округление до ближайшего деления шкалы. В качестве примера такого округления рассмотрим ситуацию, когда преподаватель, оценивая ответы большого числа учеников, ставит части учеников одинаковые, например хорошие, другой части - удовлетворительные, а третьей части - отличные оценки. Если он пользуется 5-балловой шкалой, этим качественным оценкам соответствуют 4, 3 и 5 баллов. В действительности ответы учеников, получивших одинаковое число баллов, не были одинаковыми, одни были немного лучше, а другие хуже. Учитель, даже если он был бы идеальным измерителем, определяющим знания учеников абсолютно точно, пользуясь пятибалловой шкалой, был бы вынужден округлять свои точные оценки до ближайших целых баллов. Поэтому ответы учеников, получивших 4 балла лежат между 3,5 и 4,5. Известны и другие способы округления. Например, все значения, лежащие ниже деления шкалы, могут округляться до значения предшествующего деления. Очевидно, что несмотря на различный метод округления, интервал округляемых значений будет одинаковым, и он будет равен 1-му баллу.
При оценке частных параметров и коэффициентов весомости, учитывающих важность параметров, возникает погрешность округления истинных значений до уровней, установленных на применяемой шкале. При вычислении интегральной оценки эти погрешности необходимо учитывать. Расчет погрешностей должен производиться в соответствии с теорией ошибок [11-12]. В примере с оценкой ответов учеников абсолютная погрешность округления ?s составляет ±0,5 балла. Суммарные погрешности ?s?, возникающие в результате указанного округления и вычисления обобщенной оценки, могут быть достаточно велики. На практике эти погрешности часто не фиксируются, что приводит к достаточно грубым ошибкам. Характерным примером таких ошибок является оценка знаний двух групп учеников, результаты которой представлены в таблице 3 [3].

При использовании округленных оценок, лучше подготовленной должна быть признана группа Б (14 > 13), а при оценке учащихся по их истинным знаниям, лучше подготовленной оказывается группа А (14,5 > 12,5).
Второй вид погрешностей вносится, когда применяются шкалы, по сути не адекватные анализируемой ситуации. При подсчете интегральных оценок часто не учитывается, что наиболее низкие уровни на шкале, как правило, определяют неприемлемый уровень, а наиболее высокие могут соответствовать избыточному уровню выполнения функций. В том случае, когда в список альтернатив включается ТС, имеющая оценки, соответствующие, с одной стороны, неприемлемо низкому, а с другой, избыточному уровню, интегральная оценка такой ТС может оказаться более высокой, чем у ТС с адекватным, приемлемым уровнем выполнения функций. Это приводит к ошибкам в ранжировании ТС. Для того, чтобы избежать подобных ошибок, перед сравнением интегральных оценок ТС, следует либо ТС с неадекватным уровнем выполнененя функций исключить из списка рассматриваемых альтернатив, либо выделить их в отдельную группу. Другой вид неадекватности шкал часто заключается в их линейности. Для оценки частных параметров и коэффициентов их весомости обычно используются наиболее простые линейные шкалы, хотя большинство реальных процессов и явлений описываются нелинейными зависимостями. Погрешность, связанную с использованием линейных шкал для нелинейно меняющихся свойств, как правило, трудно устранить.
Третий вид погрешностей - это случайные погрешности ?e оценок эксперта. Очень большой опыт применения балловых шкал накоплен при дегустации в пищевых производствах. Опытный дегустатор в состоянии запомнить и различить 6-10 уровней качества каждого показателя. В настоящее время 9-балловую шкалу, для которой требуются очень опытные дегустаторы, применяют только для научно-исследовательских работ, а для практических целей используют 5-балловую шкалу. [4] В других областях встречаются шкалы с количеством уровней, большим чем 9. Однако следует отметить, что, в связи с отсутствием специальных органов чувств для большинства качественных параметров, их оценка должна производиться с меньшей точностью, чем при дегустации. Поэтому для оценки таких параметров с применением шкал с количеством уровней 9 или больше необходимо использовать дополнительные качественные и количественные оценки и специальные правила их определения. При оценке по 5-балловой шкале пищевых продуктов группой специально обученных и обладающих необходимыми способностями дегустаторов считается приемлемым, если отклонение ? оценок частных параметров от средней величины не превышает ±0,5, ±1 и ±1,5 балла, соответственно с вероятностью ~70, ~95, и ~100%, однако это не всегда удается [4]. Величина этих отклонений ? должна складываться из случайной погрешности ?e оценки дегустаторов и погрешности ?s указанного выше округления. Можно полагать, что для качественных характеристик, которые не могут быть определены с помощью органов чувств или уточняющих количественных процедур, погрешность среднего эксперта не может быть меньше указанных величин. Для того, чтобы неточность оценок экспертов могла быть определена и сведена к указанному разумному минимуму, необходимо следовать достаточно сложным правилам подбора экспертов и анализа экспертной информации, например за редким исключением, каждый частный параметр должны оценивать не менее, чем 5 компетентных экспертов [3-4, 11]. Опыт показывает, что, когда речь идет о инновационных проектах, во многих случаях найти 5 компетентных экспертов очень трудно. В связи с этим в реальной инновационной деятельности погрешности экспертных оценок и, в частности интегральных оценок, могут существенно увеличиваться.
Коэффициенты весомости могут оцениваться с еще меньшей точностью, чем качественные параметры. Поскольку коэффициенты весомости, характеризующие важность параметров, не имеют опоры на объективно измеряемые показатели или качества, оцениваемые с помощью органов чувств, можно полагать, что шкала для их измерения должна быть менее точной, чем шкала для измерения параметров и, соответственно, последняя должна содержать большее число уровней. В большинстве случаев эксперты могут правильно оценить, какие функции и свойства более, а какие менее важны. Но без использования сложных вспомогательных процедур они не могут определить, насколько одни коэффициенты весомости должны быть больше других. За редким исключением у экспертов нет возможности разработать такие процедуры. Принципы разработки методики оценки величин коэффициентов весомости частных параметров ТС достаточно просты. Оценить коэффициенты весомости можно только через сравнительное "взвешивание" оценок частных параметров. Однако к сожалению, для большинства ситуаций в связи с очевидными трудностями такого "взвешивания" разработка и применение на практике такой методики будут невозможны. Поэтому, даже при самом снисходительном подходе, для оценки коэффициентов весомости, как правило, не следует применять шкалы с количеством уровней больше 5. Иногда при большом количестве параметров, характеризующих ТС, шкалы коэффициентов весомости с большим количеством уровней формируются путем сравнения важности параметров. Можно полагать, что использование в этих случаях шкал с большим числом уровней увеличивает погрешность определения как коэффициентов весомости, так и интегральных оценок. Учитывая изложенное выше, в инновационных проектах при оценке частных параметров и коэффициентов весомости считаем целесообразным принимать их абсолютную погрешность ?i равной не менее чем ±1 или ±1,5 балла.
На практике важность свойств различных объектов наиболее точно определяется рыночной ценой. В высококонкурентной экономике предложение опережает спрос, и покупатели определяют цену и, соответственно, важность множества товаров и услуг. При экспертной оценке коэффициентов весомости механизм, подобный рыночному, не работает, поэтому погрешность определяемых величин неизбежно должна увеличиваться. Насколько большие ошибки возникают при экспертном определении коэффициентов весомости, можно представить по ценовым диспропорциям, известным, например, из истории экономики Советского Союза, в котором цены на многие товары в сопоставимых величинах отличались в несколько раз от цен в странах рыночной экономики. Интегральные оценки, учитывающие коэффициенты весомости частных параметров, имеют существенно большую погрешность, чем погрешности оценок частных параметров. Поэтому в случаях, когда различия между коэффициентами весомости сравнительно невелики, целесообразно делать расчет интегральных оценок, не учитывая коэффициенты весомости.
Считается, что определение интегральных оценок оказывается относительно эффективным при количестве параметров не более 5-7. При увеличении числа параметров возрастает трудоемкость и, соответственно, погрешности ?e экспертов [3-4, 11]. К сожалению, многие системы приходится оценивать по очень большому количеству параметров. Например, такая всем знакомая ТС, как перевязочное средство (бинт, пластырь и т.д.), специалистами характеризуется с помощью 26-ти параметров [14]. Другим примером является йогурт, для оценки органолептических и вкусовых качеств которого специалисты предлагают до 32 параметров [5].
Четвертый вид погрешностей - это систематические погрешности оценок экспертов. Эти погрешности могут быть связаны с различными причинами. В отличие от случайных погрешностей их нельзя выявить статистическими методами [12]. Для инновационной деятельности проблема систематических погрешностей является фундаментальной.
Если интегральная оценка П? рассчитывается по формуле (2), ее абсолютная и относительная погрешности рассчитываются соответственно по формулам (6) и (7):
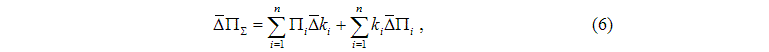
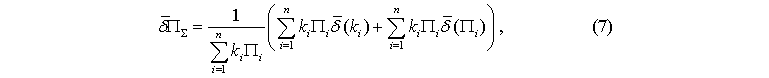
где ![]() и
и ![]() - верхняя граница абсолютной и относительной погрешностей соответствующей величины.
- верхняя граница абсолютной и относительной погрешностей соответствующей величины.
Если для оценки частных параметров и коэффициентов весомости используются 5-балловые шкалы, и абсолютные погрешности ?ki и ?Пi равны ±1 или ±1,5 балла, относительные погрешности ?П? лежат в диапазоне, соответственно, от ±40% до ±200% и от ±60% до ±300%
Как известно, относительная погрешность ? произведения равна сумме погрешностей сомножителей. Если число частных параметров ТС больше двух, то относительная погрешность ?Пп интегральной оценки Пп, вычисленной по формуле (3), будет больше, чем погрешность ?П? оценки П?, вычисленной по формуле (2). В этом случае использование формулы (3) нерационально. При использовании удельных интегральных оценок погрешность также увеличивается, если величины и в числителе, и в знаменателе не являются абсолютно точными.
Таким образом, в связи с тем, что при определении интегральных оценок, кроме погрешности округления необходимо учитывать случайные и систематические погрешности, связанные с неточностью самих экспертов, метод интегральных оценок позволяет надежно количественно отличить ТС только в очевидных случаях, когда оценки частных параметров этих ТС находятся вблизи противоположных границ шкалы. Если не учитывать погрешности оценок частных параметров и коэффициентов весомости, отличия между интегральными оценками ТС могут быть кажущимися, и их использование может приводить к грубым ошибкам. Достаточно часто эксперты, использующие метод интегральных оценок ТС, игнорируют указанные проблемы. Учитывая вышеизложенные результаты анализа погрешностей частных параметров, коэффициентов весомости и интегральных оценок, можно считать, что количественное сравнение ТС без учета указанных погрешностей является способом манипулирования или самообмана.
Выводы:
Погрешности при количественной экспертной оценке параметров ТС должны обязательно учитываться и указываться.
Без специальной методики сравнительного "взвешивания" частных параметров, которая в большинстве ситуаций является практически нереальной, невозможно количественно оценить коэффициенты весомости параметров, поэтому интегральная оценка ТС, учитывающая эти коэффициенты, является в принципе сомнительной.
При самом снисходительном подходе к оценке погрешости коэффициентов весомости погрешности интегральных оценок ТС столь велики, что, без риска совершить очень грубые ошибки, интегральные оценки можно использовать только в самых очевидных случаях.
Учитывая погрешности интегральных оценок ТС, при анализе ситуаций необходимо прежде всего ориентироваться на методики глубокого качественного а не количественного анализа, а количественный анализ частных параметров использовать как вспомогательный, хотя и важный, инструмент.
Литература
1. Альтшуллер Г.С. Алгоритм изобретения. Из-во Московский рабочий, М., 1973, 296с.
2. Минакер В.Е. Проблемы ТРИЗ в рамках реального инновационного процесса. Тезисы докладов. Научно-практическая конференция "Развитие системы подготовки преподавателей, специалистов и исследователей ТРИЗ". Международная ассоциация ТРИЗ. Петрозаводск, 2003.
3. Литвак Б.Г. Экспертная информация. Методы получения и анализа. - М. Радио и связь. 1982, с. 184.
4. Родина Т.Г. Сенсорный анализ продовольственных товаров. М., Из-во Академия, 2004, 208с.
5. Тамим А.Й., Робинсон Р.К. Йогурт и другие кисломолочные продукты. Пер. с английского, Профессия, Санкт-Петербург, 2003, 661с.
6. Функционально-стоимостной анализ в электротехнической промышленности/ В.С. Василенок, В.А. Глезер, Е.А. Грамп и др.; под. ред. М.Г. Карпунина - М.: Энергоатомиздат, 1984. - 288с.
7. Михайлова Е.А. Основы бенчмаркинга. - М.: Юристъ, 2002. - 110с.
8. L .P.Sullivan, "Quality Function Deployment", Quality Progress, June 1986, pp .39-50.
9. АЛЬТОВ Г. Шкала "Фантазия"/Г. Альтов//Фантастика и реальность. - М., 1999. - Вып. 4.- С. 5 - 17. - Центр развития образования г. Норильска
10. Г.С. Альтшуллер, Б.Л. Злотин, А.В. Зусман, В.И. Филатов. Поиск новых идей: от озарения к технологии (Теория и практика изобретательских задач), Кишинев, Из-во Картя Молдаваняскэ, 1989. 381с.
11. Лопухин М.М. ПАТТЕРН - метод планирования и прогнозирования научных работ. М. Советское радио. 1971, 161с.
12. Дж. Тейлор. Введение в теорию ошибок. М.: изд-во Мир 1985, 272с.
13. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров, М.: "Высшая школа", 1994, 544с.
14. Глянцев С.П. Требования к современным лечебным повязкам и их практическое значение / Институт хирургии им. А.В. Вишневского РАМН, Москва, Россия /Выдержки из доклада на II международной конференции. г. Москва 1995.
